Detailed instructions can be found here.
Currently available events
Group_1 contains ten events. The first five are Z -> e+e- and the other Z->μ+μ-
Group_2 contains ten events which are again Z decays into lepton pairs but this time mixed randomly.
Group_3A, 3B, 3C each contains fifty different events. The students select one of them at random. Some of them are Z decays into two leptons and the others are background events which include cosmic rays, W decays, J/ψ, Y etc.
Higgs contains twenty events seven of which are Higgs decays into four leptons and the rest are background events. The Higgs events are not real and have been constructed from a pair of Z decays, so the Higgs mass calculated is not realistic.
More events will be added in the future including real Higgs events which are currently restricted.
Select an event
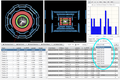
The user can select the event that he wants to view either by using the "Previous/Next" buttons or by selecting it from the drop-down list. The number of the selected event along with the total number of available events is displayed to the left of the list. Next to this, the missing energy (ETMiss) of the event, is also displayed.
Pick a track
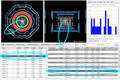
When the user clicks on a track (white line) on either of the two detector views the track is selected on both views with purple color. The corresponding line on the Track table is also selected.
The reverse is also true. Selecting a track on the Track table also selects it on both detector views.
If the track is inserted into the Invariant Mass table then it is selected there aswell.
Histograms
The histograms corresponding to the tracks of the Invariant Mass table are always automatically calculated when the user inserts or removes a track.
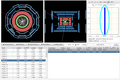

The first three histograms represent the Energy, Transverse Energy and θ angle distribution of the tracks. The next two show only the invariant masses calculated from Electron or Muon tracks. The next displays all invariant masses of pairs of tracks regardless of their type and the last histogram shows the invariant mass of groups of four tracks (either four electrons, four muons or two electrons and two muons).
By dragging the mouse below the x-axis you can either change the range of the histogram (if you drag near the edges) or move the area shown (if you drag at the center). Also after clicking on the histogram you get a blue rectangle with control points which allow you to move or resize the entire graph. The same applies to the legend.
Cuts
Cuts are limits the user can place on the displayed tracks.
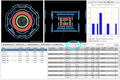
The user can select the threshold of energy of the displayed tracks. By checking the checkbox and entering a value into the corresponding field the user can remove all tracks whose energy is below the limit. Note that after entering the value, Enter must be pressed.
This can be very helpful in events with a large number of tracks where usually the low energy tracks are of no interest. However, the cut value must not be set very high as this will lead to the dissapearance of potentially interesting tracks.
Also when using the cut, high energy tracks that are part of a jet might appear as isolated and lead to incorrect identification.
Missing Transverse Momentum
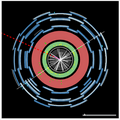
This is the momentum/energy that is not detected in the detector, but is expected because of energy and momentum conservation in the transverse plane.
The ETMiss is generally attributed to particles that escape the detector without being detected such as the neutrinos (although apparent missing energy may be caused by mismeasurement of the momentum/energy of detected particles).
In the LHC, the initial momentum of the colliding constituents along the beam axis is not known (because the energy of each hadron is split, and constantly exchanged, between its constituents), so the amount of missing energy cannot be determined. However, the initial energy and momentum in a plane transverse to the beam axis is zero, so any net momentum indicates missing transverse momentum/energy (ETMiss). It is represented (in the event display) with a dashed red line which in addition to the value (which is the magnitude of the transverse missing momentum/energy) shows the direction of the missing transverse momentum vector
Axes
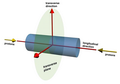
ATLAS uses a right-handed coordinate system with the z-axis along the beam pipe. The x-axis points to the center of the LHC ring, and the y axis points upwards. Cylindrical coordinates (r, φ) are used in the transverse plane, φ being the azimuthal angle. The pseudorapidity is defined in terms of the polar angle θ as η = - ln tan(θ/2).
Particle Collision Products

Some particles are very short-lived and decay almost immediately to more stable particles. In most proton collisions, the protons have gentle interactions, and the majority of the particles continue in the direction of the original particles (rather than perpendicular to the beam). However, rarely few very massive particles are produced. If particles originate from the decay of a parent particle, their tracks should join together at the same original point, called a "vertex".
Most massive particle's decays often give rise to several high-energy particles going out at large angles, more or less perpendicular to the original protons in the beam. For this reason we measure the momentum, the transverse momentum (pT), and we use it to pick up interesting events. By adding up the decay products that come from the same vertex we reconstruct the original "invisible" particle. In this exercise you will reconstruct the Z0 particle that is the carrier of the weak force responsible for the energy from the sun and radioactivity.
The Higgs Boson
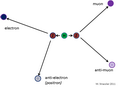
This (see Collision Products) is one of the ways in which the Higgs boson decays.
Higgs particle production and decay
A more complicated example of an "invisible" particle is the decay of the Higgs boson into two Z bosons (one of several possible decay modes). That too occurs almost instantly, and is followed by both Z bosons decaying into pairs of e+e- or/and μ+μ-.
Measurement of the width of a particle
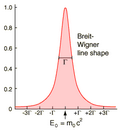
If an extremely short-lived particle is produced in a high energy collision, Heisenberg's uncertainty principle : 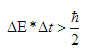
suggests that there will be a significant uncertainty in its measured energy (which means its invariant mass). The measurement of the invariant mass of an unstable particle gives a distribution (histogram) of masses called a Breit-Wigner distribution.
The width of this distribution at half-maximum is labeled Γ , Γ=1/τ, where the particle lifetime τ is taken as the uncertainty in time τ = Δt. Γ is often referred to as the "natural line width" gives very valuable information and has to be measured. As an example we quote that the measurement of the width of the Z particle in LEP (CERN's previous big accelerator which was replaced by LHC) gave a very good determination of the number of different neutrino types which exist.
Startup
When the web application is first loaded, it displays the first of the available events. The tracks belonging to this event are listed in the table at the middle of the screen (Track Table). The two detector views show the front and side view of the ATLAS detector. Next to them are the histograms of the user selected tracks (empty for now). The bottom part of the web application (Invariant Mass Table) lists the user selected tracks with their corresponding invariant masses (empty for now).

The user can interact with the web application using the buttons and controls that are available. He can also click on the tables to highlight the desired track, or click on the detector displays to pick a track.
Insert track
Since the user is trying to "discover" the Z particle from its decays into pairs of muon/antimuon or electron/positron he has to insert the selected track into the Invariant Mass table as either electron/positron by clicking the "insert electron" button or muon/antimuon by clicking the "insert muon" button. Of course in order to do that, electron and muon tracks have to be recognized first in the previous step.
By clicking the appropriate button, the selected track is copied into the Invariant Mass table and when two compatible tracks (either both electron tracks or both muon tracks) are inserted from the same event, their invariant mass is calculated automatically.
Another valid combination, dedicated to the Higgs discovery, is two electron tracks and two muon tracks or four electron or four muon tracks. Only four tracks from each event can be inserted and each track can only be used once. The user can remove a track by selecting it and clicking on the "Delete track" button.
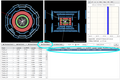
The histograms with the tracks that are inserted into the Invariant Mass table are also updated automatically. When the user clicks on a track on the Invariant Mass table the corresponding event is automatically loaded and the track is selected on both the Track table and the Detector Views.
Zoom
The user can change the zoom level to get a better view of the tracks. This can be done by dragging the zoom slider. Each view can be zoomed to a different level.
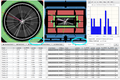
Zooming can be very helpful in events with a large number of tracks that overlap.
Discovering particles
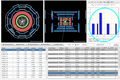
When multiple tracks corresponding to the same type of particle decay have been selected, the user can determine the mass and width of the decaying particle that produced them. In this example we have Z bosons decaying into pairs of muons.
Options
By pressing the button with the down pointing arrow the user can perform various tasks:
Import Invariant Mass Table reads a file from the local hard drive of the user and inserts the values it contains into the Invariant Mass Table. This can be useful to continue the analysis of events from a previous time without starting over.
Export Invariant Mass Table saves the current values of the table to a file in the local hard drive of the user. This file can be imported in the web application at a later time to continue the analysis.
Save histograms save the respective histogram into an image file.
Curved tracks. This option displays the magnetic field measurement window. Additionally, the tracks in the XY view of the detector are displayed with a realistic curvature which is created by the magnetic field that exists at the center of the detector. The user selects a track and then picks 3 points on it by right clicking on them. This calculates the curve radius that corresponds to those points and from that the strength of the magnetic field which is automatically inserted in the table. The top of the window displays the average value of the user measurements, the 2 pT cuts (lower and upper) and the button that displays the menu for calculating the magnetic field and managing the table contents. It also allows the user to import/export the measurements from the table.
Demo mode automatically iterates through the events of the currently selected group.
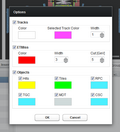
Options allow the user to select the colors and widths of all the objects that are displayed in the canvases. Also the threshold (cut) of ETMiss. This way the user can customize the web application to his personal preferences, or highlight something of importance.
Components of the Detector
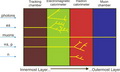
During a particle's path through the ATLAS detector, it encounters the following subdetectors:
• Inner detector (Where charged particles leave tracks)
• Electromagnetic calorimeters (Electrons and photons leave all their energy)
• Hadronic calorimeters (Protons, neutrons, pions, and other hadrons leave their energy)
• Magnet system (Bends all charged particles )
• Muon spectrometer (Only muons reach it and leave tracks)
An example of different particles interacting in different layers is shown in the above figure which shows a greatly simplified detector. The neutral particles leave traces only in the calorimeters, so there are no tracks in the inner tracking detector. On the other hand, the neutrinos are "invisible"; they do not leave traces in any component. The only way to "guess" their presence is from the missing energy/momentum, which is discussed below.
pT
The momentum in the plane perpendicular to the beams. This component of the momentum is called transverse momentum (pT). Massive particles are often produced with high pT.
Invariant Mass

The invariant mass is also called the "rest mass", and is characteristic of a particle. According to Einstein's theory, the invariant mass is a quantity which does not change with velocity or frame of reference. If the units are chosen in such a way that the velocity of light is c=1, then the invariant mass is defined as
![]()
where E is the energy and p = m*ν the momentum of the particle. To determine the invariant mass of a particle which decays almost instantaneously, one has to look at its decay products. One has to measure the energy and momentum of each decaying particle and then sum all their energies
E = E1 + E2 + E3+ ...
and their momenta
![]()
The result is the invariant mass and if you are looking at one particle, then the mass calculated in each event should be "almost" the same, so if you make the distribution of masses for various events you will see a peak around the particle's mass.